Published by Catfish3

Feb 23, 2013 (last update: Mar 18, 2013)

Score: 4.3/5 (78 votes)

• The LZ family of algorithms
• Goal
• Language
• Lossless compression versus expansion
• Entropy, and dictionary coders
• The LZW algorithm
• Version 1
• Version 2
• Version 3
• Version 4
• Version 5
• Version 6
• Ending notes
• Useful links
• Thanks go to

The LZ family of algorithms

Abraham Lempel and Jacob Ziv published two compression algorithms: LZ77 in 1977 and LZ78 in 1978.

Terry Welch published the LZW algorithm in 1984 as an improvement of LZ78.

LZW is just one of the original LZ algorithms' many derivatives, the more famous ones being LZSS (used in RAR), LZMA (used in 7z), and Deflate (used in ZIP).

This article is about LZW because:

• it's easy to understand and to code, yet
• it offers decent compression ratios and speed, and
• its patents have expired

Goal

The goal is to implement an LZW file compressor, and gradually improve it.

Alpha versions:

• Version 1 [ Jump ] [ Download ]
  Straightforward but slow implementation. The encoder uses a plain map. The decoder uses a string vector.
  


• Version 2 [ Jump ] [ Download ]
  Faster compression. The encoder uses a hash map. The decoder is reused from Version 1.
  


• Version 3 [ Jump ] [ Download ]
  Faster compression and decompression. Both the encoder and the decoder do pair mapping, instead of string mapping.
  


• Version 4 [ Jump ] [ Download ]
  Faster compression and very fast decompression. The encoder uses a custom memory allocator. The decoder is optimized.
  


• Version 5 [ Jump ] [ Download ]
  Very fast compression and decompression. The encoder uses a vector-based binary search tree. The decoder is reused from Version 4.
  

Beta versions:

• Version 6 [ Jump ] [ Download ]
  Uses variable width codes. Compared to Version 5, it's significantly slower but compresses better.
  

The above programs are command-line utilities. Their source code is attached to this article as ZIP archives.

Notes:

• The programs perform better if compiled with optimizations turned on.


• I currently use MinGW (GCC 4.7.2) and compile by running:
  g++ -Wall -Wextra -pedantic -std=c++11 -O3 lzw_vX.cpp -o lzw_vX.exe

Language

The source code is written in C++11, the 2011 version of the C++ language's standard.

Your C++ compiler must support lambda functions, range-based for() loops, and initializer lists, for to successfully compile the source code snippets in this article, and the full programs attached.

Lossless compression versus expansion

Given data D of size S_D, the intent is to encode it as data E of size S_E, such that:

• S_E < S_D
• E can be decoded as D

If S_E is less than S_D, compression was achieved.
If, in addition, the original data D can be reconstructed from E, the compression is lossless.

Notes:

• The compression ratio is computed with S_E / S_D.

Expansion is the opposite of compression, with S_E > S_D.

Expansion occurs because it is mathematically impossible for a lossless compression algorithm to compress all files. This is proven with the counting argument, which you can learn more about by following the designated link at the bottom of this article.

A simplified, crude example:
The example above shows that, because a lossless compression algorithm needs to produce a distinct encoded file for each data file, not all data files can be compressed -- and in fact, some of them will be expanded.

For instance, what can "0" be compressed to? We cannot reuse the outputs for "", or "00", or "01" because then how will the decoder know which file to decode?

This is the crux of the counting argument: if all files can be compressed, the total number of unique compressed files will be less than the number of uncompressed files, which means there's no one-to-one correspondence between them, which means the compression algorithm is not lossless.

Entropy, and dictionary coders

For our purposes, entropy is a measurement of the unpredictability of data. Data with low entropy tends to have repeating sequences. Data with high entropy tends to be random.

A dictionary coder is a lossless compression algorithm that takes advantage of low entropy. It associates sequences of data with codes (which use up less space) in a "dictionary". Compression is achieved by substituting repeating sequences with their corresponding codes. The longer the sequences replaced, and the higher their frequency, the better the compression.

Notes:

• Text files tend to have low entropy.
• Multimedia data files and archives tend to have high entropy.

The LZW algorithm

LZW is a dictionary coder. It starts with a dictionary that has entries for all one-byte sequences, associating them with codes. The dictionary is updated with multiple byte sequences, as the data file DF is read. The encoded file EF will consist entirely of codes.

For simplicity, byte sequences will be referred to as "strings".

The type used to store codes will be CodeType.

Notes:

• In the C++ language, char is defined to be a byte.


• On most computers, a byte has a width of eight bits.


• A bit can hold a value of either 1, or 0.


• The CodeType can be anything wider than a byte.


• A map is a data structure that associates a value, "key", with another value, "element".


• Arrays are a special case of map, where a numerical code (index) is associated with an element, e.g.:
  dictionary[14] == "cat"


• The encoder's dictionary is a map that associates a string with a numerical code, e.g.:
  dictionary["cat"] == 14

Encoder pseudocode:
Simplified run of the encoder:
It stands to reason that the decoder must use the same dictionary that the encoder had used, otherwise DF cannot be recovered from EF. To solve this problem, DF is encoded incrementally, the encoder thereby ensuring that the decoder will have enough information to rebuild the dictionary.

Decoder pseudocode:
Simplified run of the decoder:
The decoder first has to deal with bad input. Because DF is encoded incrementally, a valid code can never exceed the dictionary's current size. Therefore if such a code was read, the decoder must give up.

Then the decoder has to deal with the special case, of being given the code for the very string it's supposed to add in the dictionary.

This artifact only occurs when the encoder deals with the pattern cScSc, where c is a byte and S is a string, and the encoder already has cS in the dictionary. The code for cS will be written to EF, and cSc will be added to the dictionary, and in the next iteration the code for cSc will be written to EF. The decoder deals with this situation as shown in the pseudocode: an entry is added for cS + c, where cS is the previously decoded string and c is its first byte.

Version 1

The pseudocode above paves the way for a straightforward implementation. There is, however, one missing detail: what type should CodeType be? The only remark so far was that it must be wider than a byte. The reason for this is that the dictionary still has to be able to grow, after it is filled with codes for all strings consisting of a single byte (256 entries). If CodeType were a byte, the dictionary could hold exactly 256 entries, all of which would be filled in at the beginning, and then the dictionary couldn't grow.

A sensible type to use is one with a width of 16 bits, such as unsigned short int, or uint16_t for clarity. Now the dictionary can accommodate a total of 65,536 entries, out of which 65,536 - 256 = 65,280 are new entries.

One may be tempted to use a 32-bit (or a 64-bit) type such as uint32_t (uint64_t), which would allow the dictionary to store a humongous number of entries. In practice, this degrades compression because each code written to EF would require 32 (or 64) bits to store, and a lot of those bits wouldn't be used anyway. In addition, the dictionary would keep growing until it used up all of the computer's memory.

Speaking of dictionary growth, at some point the 16-bit dictionary will become full. This can be dealt with by resetting it to its initial state of the first 256 entries. The encoder and decoder are merely added a check at the beginning:


In the C++ source, the resetting is done by a named lambda function (they are usually anonymous). The reason behind using a lambda function, embedded into the encoder, is that the dictionary reset function must be custom made for the dictionary, and will never be used outside the encoder.

[ Download Version 1 ]

Version 2

The first version has a performance issue: it takes too long to compress and decompress big files.

Let's assume that the cause of the slowdown is input and output, that is, file reading and writing. C++ file streams are already buffered internally, so let's assume that the buffers are not large enough. Because the streams allow custom buffers to be used, we proceed to use two 1 MB buffers, one for the input file, the other for the output file.

Example code:

This indeed has the effect of reading and writing files in 1 MB chunks, greatly decreasing the total number of reads and writes. However, the program remains slow. It appears that the original assumption was wrong, and I/O isn't the bottleneck.

Due to the simplicity of the program, it can be deduced that the slowdown occurs in the encoder and decoder.
Both the encoder and decoder make heavy use of strings. Appending bytes to a string is likely to trigger memory reallocation and the subsequent copying of data to the new location.

The encoder can be improved by using something other than std::map. The C++11 standard added std::unordered_map, which behaves like std::map, with the exception that it hashes the key (which is what makes it a "hash table"). Hashing can be summarized as follows: transform something (in our case, the string) into a hash code (a number) unique to it.

When a hash function obtains the same hash code for two different inputs, that is called a hash collision. Good hash functions have few collisions, bad hash functions has many collisions, and perfect hash functions have no collisions. The latter are outside our reach, because each possible string encountered must turn into its own unique hash code, and we can't use a hash code type wide enough to accommodate for that.

The purpose of the previous paragraph was to serve as a prelude to saying that this version of the program can theoretically corrupt data. Although the 16-bit dictionary's limit of 65,536 entries should make collisions very unlikely, they are still possible. What we get in return for this is faster code retrieval, which means faster compression.

Before we can use std::unordered_map, a hash functor must be written to handle std::vector<char>.

Fortunately, there already exists an std::hash functor to deal with std::basic_string<char> (more commonly known as std::string), that can be reused. The rest of the code remains unchanged.

Example code:

[ Download Version 2 ]

Version 3

So far, not much was done for the encoder, and nothing at all was done for the decoder. Clearly, it's time for a change; if the algorithm and the associated data structures produce a slow program, what's the point in trying to optimize the program?

Let us consider what we've learned so far:

• The encoder isn't required to store the actual strings in the dictionary.
• The LZW encoder pseudocode shows that any new string added is the result of appending a byte to an already existing string.

Plain English translation: goodbye strings!

The plan is as follows: the encoder's dictionary will no longer map a string to a CodeType. It will map a pair (CodeType, byte) to a CodeType instead.

The initial single-byte strings will be represented as a pair of an invalid CodeType and the given byte. That "invalid" code must be a value that can never appear in EF. A fine choice is the dictionary size limit, which in the source is globals::dms. Because the dictionary is reset when it reaches that size, an entry mapping to that code will never be generated.

Encoder pseudocode:
On most computers, this pair-based algorithm will run faster than the previous string-based ones.

Now we have two choices with regards to the decoder.

1. leave it as it is
2. try to remove strings from it as well

The first option is possible because all three programs so far generate an identical EF out of the same DF (and vice versa). So the decoder could be left as it is, and the program would still decompress files correctly. However, the promise of faster decompression speeds is tempting.

We start with an array consisting of all the pairs of invalid_code and a unique byte, which will be the dictionary. As EF is read, new entries will be added, consisting of a valid code and a byte, the code representing the existing string to which the new byte is appended.

At this point it should be obvious that to reconstruct the strings, we will use the code information to chain together the attached bytes. This is done by a new lambda function named rebuild_string().

Simplified dictionary mechanics:
Notice that the rebuilt strings will be reversed.

Decoder pseudocode:
The source code for the above decoder is structured differently in the actual program, because a string variable was introduced, to ensure that the k string is only "rebuilt" once.

[ Download Version 3 ]

Version 4

The decoder is still slow because the string that the rebuild_string() lambda function produces is passed by value. This means the s variable has to be allocated space for, as it copies the contents of whatever string the lambda function returns.

The optimization in the decoder becomes clear: s becomes a string pointer, and rebuild_string() returns the memory address of the now static string it produces internally. The only thing that's copied is the string's memory address (basically a number), which is a very cheap operation.

Because of this change, the decoder becomes extremely fast, and personally, I feel it's finally optimal.

The encoder, however, still has a long way to go. In its current form, the best that can be done is to try and cut down on std::map's repeated internal memory allocations. This is achieved by using a custom memory pool allocator.

An allocator is a class that manages memory. Containers such as std::map normally use the default built-in allocator, but can be given a custom one to use instead.

The goal is to allocate memory as rarely as possible. An allocator with this goal would get a big chunk of memory (the pool), then give out smaller chunks of this pre-allocated memory when the container requests them, instead of actually getting new memory.

Writing our own allocator is no picnic, and pretty soon we'd be in deep, trying to optimize it.

So we'll just use a ready-made allocator instead. FSBAllocator by Juha Nieminen is an excellent choice (see the links for more information). Version 4 bundles this library so a separate download isn't required.

[ Download Version 4 ]

Version 5

In Version 4, the custom allocator alleviates the performance penalty induced by memory allocation. Therefore, if the program is still slow, it can only be that std::map is still slow.

The standard library's std::map served us well, but if encoding speed is to become optimal, a custom dictionary data structure has to be coded, designed for the LZW algorithm.

There's nothing wrong with the actual encoder algorithm. What we set out to do is write an EncoderDictionary class that functions faster than the current std::map<std::pair<CodeType, char>, CodeType>.

The encoder can be simplified by adding extra functionality to the EncoderDictionary class. Two obvious improvements would be:

1. Make it so that the dictionary resets itself automatically.
2. Search for and insert a new element in a single pass.

Thus, the encoder pseudocode is much simplified:


The above algorithm should look familiar because it's based on the pair encoder of Version 4.

The commented else branch isn't needed because ed.search_and_insert() already updates i to the index of (c, i) if the pair was found, otherwise sets i to invalid_code.

The new dictionary also initializes itself and resets when full, so the lambda function reset_dictionary() isn't needed anymore, either.

With this out of the way, we can focus on implementing EncoderDictionary.

Everybody seems to be using binary search trees to improve the performance of their LZW encoder. I've attempted an index-based solution (no searching, at the price of greater memory consumption), but I was disappointed with the performance, although it was still faster than Version 4.

In the end, I decided to implement EncoderDictionary as a vector-based unbalanced binary search tree, with much inspiration from Juha Nieminen's article.

A binary search tree (BST) is a data structure which consists of linked nodes. Any node has one parent node, and at most two children nodes. (The root node is the exception, in that it doesn't have a parent.)

A node contains data, in our case a byte. The left child node will contain a byte of lesser value than the parent node's. The right child node will contain a byte of higher value.

The tree is unbalanced if its branches vary in depth with more than one level. This degrades search performance in big trees, which is why usually an extra effort is made to balance the tree. In our case, the tree will be too small for the performance to significantly worsen.

Finally, being vector-based means that nodes are stored in an std::vector which pre-allocates the needed memory, as opposed to the nodes spawning their children via dynamic memory allocation. The effect is comparable to using FSBAllocator in std::map.

Figure of an unbalanced BST:

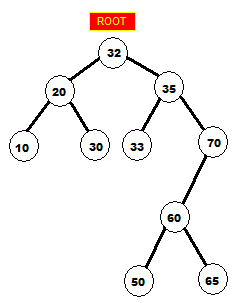
Notice how all the left-hand descendants (left subtree) of a node contain lesser values, and the right-hand descendants (right subtree) contain higher values, than that of their ascendent node.

Let's search the tree for the value 65.


It took 5 comparisons to find a value in a tree that has 10 nodes. On such a small scale it's hard to see the search speed improvement, but it will become very obvious when we'll use the program on multi-megabyte files.

Figure of a balanced BST:

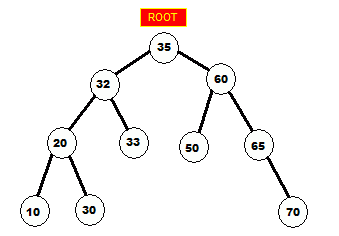
This is how the unbalanced tree could look if it was balanced. Notice the depth of the branches (levels).

To reiterate, balancing the tree is an extra effort in our case, it is not truly warranted and will therefore not be pursued.

Back to EncoderDictionary, it's obvious that the member function search_and_insert() is very important. It has three chores:

1. If the vector of nodes is full, reset it.
2. If the pair (c, i) was found, return its index.
3. If the pair (c, i) wasn't found, add it to the vector of nodes and return invalid_code.

The vector of nodes is an std::vector<Node> where Node is a structure defined inside EncoderDictionary:



The comment for first may be misleading, as it doesn't refer to children nodes, but to the index of the first node to use the current node's data as a prefix string.

Remember how in Version 4, a pair (CodeType, byte) was mapped to a CodeType? This is what happens here as well, with the twist that the codes are linked to each other by the nodes, which increases the search speed.

EncoderDictionary::search_and_insert() code:

It should be obvious what reset() does.

search_initials(c) is essentially an optimized equivalent of a possible search(c, globals::dms) function, returning the index of initial one-byte strings.

[ Download Version 5 ]

Version 6

A decent compression rate (speed) was attained in Version 5. Now the focus will shift on improving the compression ratio.

Theoretically, if we allow the dictionary to hold more than 64 Ki entries, we'll get better compression. But then CodeType will need to be widened from 16 bits in order to access those entries.

Let's remember why we settled for a 16-bit code type in the previous five versions (which will be called "alpha versions" from now on). The reason was that the codes written to EF would waste more space than they'd save, and thereby worsen compression. Space would be wasted because the codes would be wider than needed, leaving bits unused.

To illustrate this, consider the encoding of a CodeType with the value 375:

Technical accuracy disclaimer:

• Endianness isn't the topic of this article.

Notice that while 8 bits can't store the value 375, a CodeType of 16 bits would waste 7 bits, and a CodeType of 32 bits would waste 23 bits. The ideal width to store the value 375 is obviously 9 bits.

The plan is as follows: use a 32-bit CodeType, and a dictionary holding at most 16 Mi (16 * 1024 * 1024) entries, while at the same time only reading and writing as many bits as needed for the codes.

Notes:

• A dictionary holding 16 Mi entries will use more than 16 MiB.
• The reason for this is that an entry consists of more than a mere byte.
• The encoder will use about 256 MiB, if sizeof (Node) == 16 bytes.
• The decoder will use about 128 MiB, if sizeof (std::pair<CodeType, char>) == 8 bytes.

This approach of using variable width codes is feasible because we can we can always verify how many bits are needed to encode the largest code in the dictionary, and adjust the code input/output width accordingly.

The tricky part will be implementing the custom I/O system, on top of the old one which only understands bytes and things that you get by putting bytes together.

The goal is writing custom CodeWriter and CodeReader components, that the encoder and the decoder will be adapted to use instead of bare std::ostream and std::istream.

---

A few days pass, as I struggle with the custom I/O system, and it struggles with me.

---

Reading and writing variable width codes is a fair amount of work, which involves shifting and masking bits, and saving the current incomplete byte until enough bits are read/written.

I had to choose between two code splitting layouts: LSB-First (least significant bit first) and MSB-First (most significant bit first). See the Wikipedia article on LZW for more information on packing order.

Notes:

• MSB-First is easier to visualize and is more intuitive.
• LSB-First is less intuitive but I found it can run faster than MSB-First, and it seemed easier to implement.

There's no reason to list the source code of CodeWriter and CodeReader here. The classes are ugly, cryptic, and just barely work. They also uglify the compress() and decompress() functions, because of the extra code that is needed to synchronize the bit widths.

The essence of CodeWriter and CodeReader is that they can write and read codes of variable binary width, ranging from a minimum of 9 bits up to a theoretical maximum of 32 bits, which will never be reached because of the dictionary limit.

The plan involving the huge dictionary had changed. Nobody stops you from changing globals::dms back to 16 Mi, but if you want my advice, 16 Mi is too much.

A big dictionary can degrade the compression ratio, which might seem illogical, yet is expectable if code widths grow so much that it becomes cheaper to use shorter codes from a smaller dictionary.

Using a big dictionary will give better results for files with high entropy, but in that usage scenario the given file will most likely be expanded anyway.

I have decided that a sensible dictionary entry limit is that of 512 Ki (512 * 1024). The program remains reasonably fast, although is obviously slower than Version 5, while almost always providing better compression ratios. At least this version can finally compress license.txt in case you didn't notice that the alpha versions can't.

You are welcome to try different limits. Obviously, a low limit such as 64 Ki will create a program that consumes roughly twice as much memory as Version 5, while being quite fast. Reverting to a 16-bit CodeType and using a limit below 64 Ki will further improve speeds, but worsen compression.

In my tests, Version 6 with a 32 Ki dictionary limit and 16-bit CodeType outperformed Version 5 in both compression speed and ratio.

A higher dictionary limit will slow down the program, yet it doesn't mean that better compression will always be achieved, although it usually is. It all revolves around the nature of the file to be compressed.

Notes:

• Should you experiment with different dictionary sizes, please remember that for an encoded file EF you should decompress it with the same program that you used to compress it.


• Otherwise, decompression will probably fail.

[ Download Version 6 ]

Ending notes

I apologize that toward the end, this article became wordy. I intend to keep updating it, and to add new versions, while compacting the text.

Remember that these programs are merely toys which will misbehave for data with high entropy (such as compressed archives, MP3s, AVIs, and other media). In fact, one should expect the resulting archive to be much larger than the original file, in this usage scenario. Best compression ratios are usually achieved for text files.

The programs compile with nuwen's MinGW distro 9.5 (GCC 4.7.2), see the links below for download.

The attached ZIP archives bundle the program's source code and its Doxygen documentation.

Please let me know (via PM) if you find bugs, spot mistakes, or otherwise have suggestions for improving this article and the attached programs. Thank you.

Useful links

LZW and compression in general

• http://en.wikipedia.org/wiki/Lempel%E2%80%93Ziv%E2%80%93Welch
• http://marknelson.us/2011/11/08/lzw-revisited/
• http://www.cs.duke.edu/csed/curious/compression/
• http://warp.povusers.org/EfficientLZW/index.html
• http://en.wikibooks.org/wiki/Data_Compression
• http://mattmahoney.net/dc/dce.html
• http://www.data-compression.com/index.shtml

The counting argument

• http://www.faqs.org/faqs/compression-faq/part1/section-8.html

C++11

• http://en.wikipedia.org/wiki/C%2B%2B11
• http://wiki.apache.org/stdcxx/C%2B%2B0xCompilerSupport

Software

• http://nuwen.net/mingw.html
• http://warp.povusers.org/FSBAllocator/

Miscellaneous

• http://en.wikipedia.org/wiki/Mebibyte

Thanks go to

• cire
• Cubbi
• Duoas
• JLBorges
• Peter87
• Velnias75

Attachments: [lzw_v1.zip] [lzw_v2.zip] [lzw_v3.zip] [lzw_v4.zip] [lzw_v5.zip] [lzw_v6.zip]